Late last century I wrote about three mathematical ideas that hold particular interest for me. (See an earlier Math posting for a web link.) All have to do with the basics of number and structure. I went into some detail about ideas,
* the “balanced base 3” about which I wrote yesterday,
* and “N-Grams”, a collection of diagrams formed using the same mathematical/diagrammatic rules/conventions as the Enneagram, but applied to varying number bases and divisors. I’ll say more in another post.
This post is about alternate coordinate systems, in addition to the familiar Cartesian system, in which each axis is at right angles to every other axis.
The terminology I use is xMy where x is the number of axes and y the number of dimensions being measured. Cartesian coordinates are 1M1, 2M2, and 3M3 in 1, 2, or 3 dimensions.
Zero-balanced coordinates
There is a 2M1 system, a 3M2 system and a 4M3 system in which all the coordinates add to zero for any point in (1, 2, or 3 dimensions of) space.
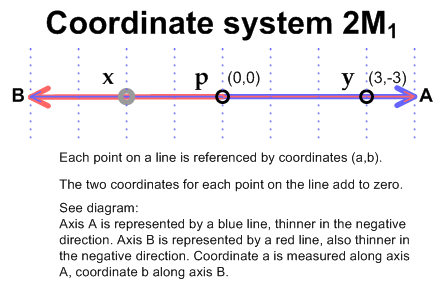
2M1 is simply a standard Cartesian single dimension paired with its mirror opposite.
3M2 has 3 axes oriented on a plane from the center of a triangle towards its three corners (or towards the centers of its three sides). Here is a graphic representing the 3M2 system.
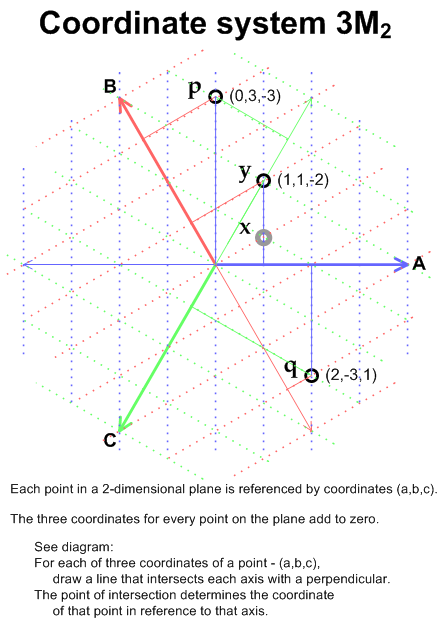
Coordinates are given in the diagram for points p, q, and y. Point x is precisely between p and q – hence, its coordinates can be determined by averaging the coordinates of p (0,3,-3) and q (2,-3,1). So x is at (1,0,-1).
4M3 has 4 axes oriented in 3D space from the center of a tetrahedron to its four vertices (or towards the centers of its four faces).
*** This post became content for a page on this site. Go there for more on this topic. ***
Connections Elsewhere
Fuller gave the name to the Vector Equilibrium because he perceived it to be the shape right at the balance point between being inward focused and outward focused (this is a rough approximation of his idea) – at an equilibrium point between imploding and exploding. The pattern of its edges and the struts between center and vertices ARE an octet truss. Flooring made with an octet truss has some rather interesting engineering attributes – such as the way it distributes a load put at any point on its surface.
Kirby Urner has a different take on what I call 4M3. He named his form quadrays. More info on this can be found at www.grunch.net/synergetics/quadrays.html.