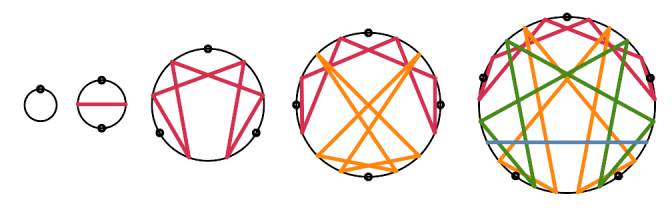In my last post I described N-Grams as “a collection of diagrams formed using the same mathematical / diagrammatic rules / conventions as the Enneagram, but applied to varying number bases and divisors.” Here are the N-Grams for base ten – that is, the patterns formed when dividing by various numbers in base ten. Note the gray circles at 2, 4, 5, 8 and ten – the prime factors of these numbers (2 and/or 5) are the factors of the base used for these diagrams, ten. The circle for 6 is partially gray, because the prime factor 3 generates a repeating pattern, whereas the prime factor 2 does not.

I am moving this material to a page on this site, leaving this (somewhat edited from the original) post as a place for comments.
I put some material about N-Grams on the web (~Sept. 2000) at www.solbakkn.com/math/n-grams.htm . Most of that is now here in posts and pages, so may go away some day.
I’ve corresponded with Shane Roberts who has taken the same idea in a similar direction, calling his diagrams Rotagrams. Shane said I could share his email, (may not be current) systemlover at hotmail dot com. His diagrams include non-repeating patterns, e.g., .125 for 1/8 (base ten) and fractions where the divisor is larger than the number base being used to represent the fraction, mine do not.