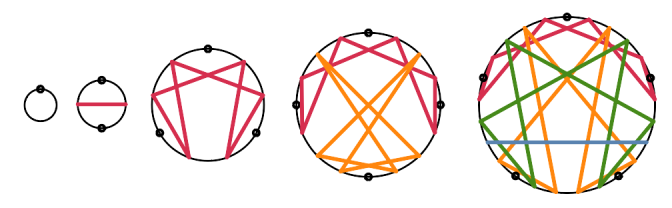N-Grams
The structure of the Enneagram is what led to my exploration of N-Grams. The patterns in the Enneagram are related to division by 7 and by 3 using base ten, which we humans use for most of our arithmetic. (There’s also base 12 in a dozen and a gross; base 60 in seconds and minutes, etc.) Many years ago Anthony Blake showed a group a 16-gram (based on division by 4 and 13 in base 17 — the 4th of 5 figures in my site header). That got me interested in exploring the patterns of repeating digits that form in other number bases, and finding graphic representations for those patterns. Without Tony’s encouragement, it’s likely I wouldn’t have taken the effort to produce these diagrams.
Each of the figures I call N-Grams is based on the digit patterns that form for a given number base and divisor. The Enneagram uses base ten (with 9 numbered locations around its circular circumference) for the repeating patterns of digits in the fractions 1/3 (0.333…, 0.666…, and 0.999…/0.000…) and 1/7 (0.142857142857… and the ever-present 0.999…/0.000..).
The top point of each N-Gram represents both the smallest and largest digit for the relevant number base – 0 and 9 for base ten. When dividing by any integer less than the base, no repeating patterns use these digits (except for 0/N = 0.000… and N/N = 1.000… = 0.999… – for bases other than ten, replace the “9” with that base’s largest digit). I use a somewhat different convention than the usual diagram of the enneagram. Rather than a triangle, I use small circles at the top 0/9 point and at 3 and 6 (1/3 = 0.333…, 2/3 = 0.666…) since each represents a single repeating digit.
When there are limited or no repeating patterns of digits produced by a division, the resulting N-Gram is partially or fully gray. These occur when the number base and the divisor have a prime factor in common. The following diagram shows the N-Grams for base ten. (These form one row in the “by number base” diagram.) The number under each is the divisor for that N-Gram.

Note that the circles for 10, 8, 5, 4, and 2 are fully gray. All the prime factors (2 and 5) for these divisors are also prime factors for base ten. Hence the division quickly “zeroes out” (e.g., in base ten, 1/5 = 0.2000…, 1/4 = 0.25000…). The circle for 6 is partially gray, because its prime factor 3 generates repeating patterns (2/6 = 0.333…, 4/6 = 0.666…), whereas its prime factor 2 does not.
The first two tables below have one row for each number base; the second is a “folded” version of the first, followed by the row for base 17. I found it interesting that the overlapping patterns never (except for the top point) “step on each other’s toes” – each uses a different subset of the available digits, and together use all of the digits.
The third table has rows for each divisor. After that is a discussion of “S-Grams,” some animations, and other related matters.
N-Grams by Base
Each diagram below graphically represents any digit-patterns formed when dividing by some number in an equal or larger number base. Each row of diagrams below show the results of division using a given number base, the base shown in the left-most diagram. This organization points out many regularities in the patterns. For instance, division by a number one less than the base yields single-digit repeating patterns (e.g., in base ten, 1/9 = 0.111…, 5/9 = 0.555…). There is also a strong regularity in the patterns on either side of the vertical center line for the odd-numbered bases (when paired – see the Paired N-Grams table – they form the right-most figure for the odd-number bases).
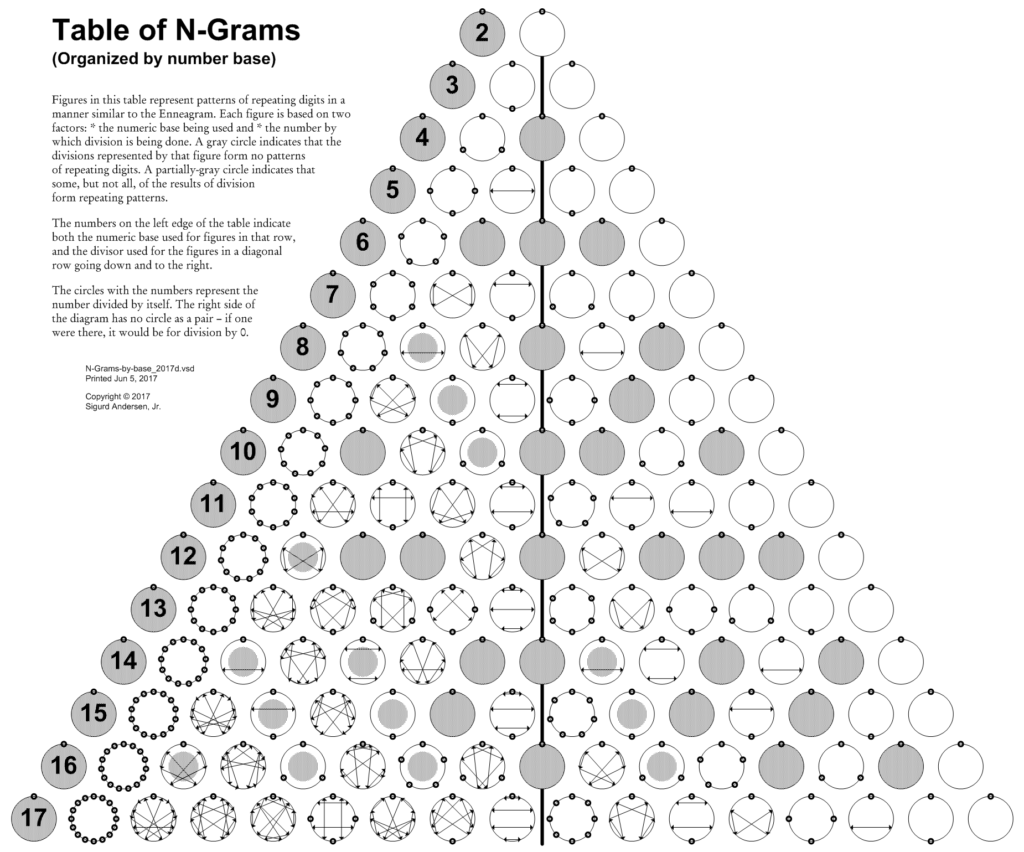
Paired N-Grams
The diagram below takes the N-Grams by Base diagram (above) and folds it in half. The simpler patterns that were on the right of the center line are displayed in red below. The result is a pair of patterns that (whenever the two divisors have no prime factors in common with the number base) use every digit once (the exception being the top point, which occurs in every N-Gram.

(row for base 17 added 2023 – may add 14-16 at some future date)
N-Grams By Divisor
To track the patterns from a single divisor in the N-Gram by Base table, the path is down and to the right from that number on the left edge. In the Paired N-Grams table, the downward path “bounces” to the left when the base reaches double the divisor, after which the divisor is the smaller of the divisors in the pair.
The next arrangement of the N-Grams puts the patterns for each divisor in one row of the diagram. It brings out (through base 5, anyway) how each pattern in the row repeats regularly. The sequence of distinct patterns repeats with each multiple of the divisor. The first pattern, where the divisor is the same as the number base, yields only the top-point pattern that is in every N-Gram [ N/N = 1.000…=0.999… ]. This is the “null” pattern, with minimal repetitive activity. This patter recurs whenever all the prime factors of the divisor are also prime factors in the number base. Examples are division by 4, 8, or 16 in any even-numbered base, or division by 9 or 27 in any base divisible by 3. When the number base is one more than the divisor, you get the same simple pattern for every divisor – a repetition of a single digit. For instance, in base ten, 1/9 = 0.111…, 2/9 = 0.222…, and so on. The set of N distinct patterns formed by division by N repeats starting at 2N, at 3N, and so on. For instance with division by 5, the patterns for[ 6, 11, 16, …] are basically the same, as are the patterns for [7, 12, 17, …] and [8, 13, 18, …] and [9, 14, 19, …].

Second Power N-Grams (S-Grams)
There’s a particular sequence of paired N-Grams that I call second power N-Grams; Tony Blake calls the figures in this sequence S-Grams. In this discussion I will use the names S1, S2, etc. for: the 1-gram (S1), 4-gram (S2), 9 (ennea)-gram (S3), 16-gram (S4), 25-gram (S5), … (having respectively 1, 4, 9, 16, 25, … points around the perimeter, representing bases 2, 5, 10, 17, 26, …) with divisions by 1&1, 2&3, 3&7 (the enneagram), 4&13, 5&21, …. The header of this site has images of the first five of these.
I’ve put the numerical sequences for the figures S2 through S11 (4-gram through 121-gram) in a revised PDF. (previous PDF, A4-sized) that now includes the “informing” digits (the black dots in the diagrams below) as well as the “resolving patterns (colored lines below). you will see that almost all of the patterns are of length 6, with a new pattern of 2 (from the fraction 1/3, which shows up as 7/21, 19/57 and 37/111) in every third S-Gram (S2, S5, S8 and S11). The pattern of 2 in S2 grows, in the following S-Grams, to a pattern of 6, then to 2, 3, 4, … patterns of 6. The new patterns of 2 in S5. S8, S11, … each grow in the same manner. By the time we get to S11 (base 122), there are 9 patterns of 6 “grown” from the first pattern of 2, 6 patterns of 6 from the 2nd, 3 patterns of 6 from the 3rd, and a new pattern of 2 that will grow as have the others. When I first encountered this extreme regularity, I was surprised. I will be trying various animations for some of these (see below).
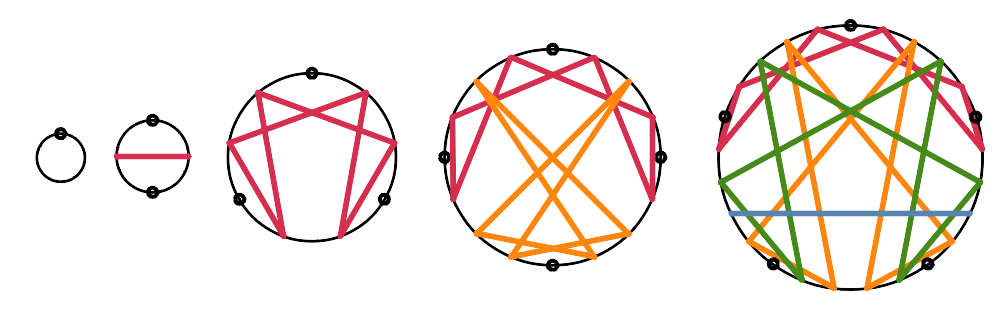
The figure above starts at the left with the simplest of the S-Grams, S1 (in perhaps-mystic terms there is an “invisible” S0 to its left) through S5. These figures have no arrows to indicate direction of flow. The colors were meant to bring out the growth of the length 2 and 6 sub-patterns.
Animations
Division by 7 in bases 10, 17, 24, and 31
To make it easier to see what changes with an increasing number base, I’ve constructed two ways to show division by 7 in bases 10, 17, 24, and 31. [The # animated GIF is more nimble, the # matched web pages let you wait and then click to see the next image in sequence, but loading a new web page for each click makes it slow. Once they’ve each been loaded, going back & forth is nimble.] Each diagram in the sequence shows division by 7 as a pattern in red. The complementary pattern (that touches all the other points around the circle) is represented by 3 black dots in base 10, and by blue lines in the other bases. The figure in base 31 and in base 10 (last and first figures in the sequence) have in common 3 anchor points which are in precisely the same points in the two diagrams. The blue complementary pattern in base 24, division by 17, yields a single figure with 16 points along its path (and, the ever-in-common top point). The complementary pattern in base 31, division by 24, yields 9 pairs of points (2-digit sequences) and 6 single points (at 0, 1/6, 1/3, 1/2, 2/3, and 5/6).
S-Grams
The header for this site has figures S1 through S5; this # animated GIF cycles through the figures for S5, S6, and S7.
To highlight sequences within one figure, this # animated GIF (for #7) has 1/43, 2/43, 3/43, 4/43 and 5/43 in red and the sequences for 9/43 and 10/43 in blue. Together, these seven patterns of length 6 (along with the ever-present zero-point) cover all the manifestations of dividing-by-43 in base 50.
Other references
For the time being, you can find some of what I wrote decades ago on N-Grams at www.solbakkn.com/math/n-grams.htm .
Shane Roberts has taken the same idea in a similar direction, calling his diagrams Rotagrams. He has produced a CD titled Number Nature: An Introduction to Rotagram Systems. It is referenced at OCLC WordCat and the National Library of Australia’s catalogue. His diagrams differ from mine in that they include non-repeating patterns, e.g., .125 for 1/8 (base ten) and division by numbers larger than the number base.
For exploring divisions by numbers larger than a number base, I would suggest it would be fruitful to use powers of the number base. For instance, rather than over-driving base 3, use powers of 3: 9, 27, 81, 243 – I’d start with the smallest power of 3 larger than the divisor. This would bring order to the otherwise chaotic-appearing sequences. For instance, in base 27, each digit represents a unique 3-digit sequence in base 3.
Balanced Odd Base N-Grams
For odd number bases using balanced digits (see Balanced Ternary), NGram-like patterns are going to be somewhat different – see this page.